MATIKA

DERIVACIE 

Uz viackrat sa tu objavili requesty na pridanie rubrik o derivaciach a integraloch, tak nech sa paci, mate to tu  Sice to trvalo nejaky ten pondelok, ale lepsie neskor ako nikdy 

Nebudem tu davat odstavce s teoriou pretoze asi to vecsinu z vas nezaujima, ale je dobre mat aspon prehlad o tom co vlatne pocitame a naco to je dobre.

Derivaciou tak ako limitami zistujeme priebeh funkcie. Vieme urcit derivaciu v bode v ktorom existuje, jej rast ci pokles v specifickych bodoch a taktiez lokalne extremy maxima a minima.  Pozname derivacie prveho druheho az x-teho stupna a taktiez derivacie parcialne podla jednotlivych premennych. Su to najzakladnejsie operacie s derivaciami ktore sa na skole ucia a je dobre mat v nich prehlad. 

Takze na zaciatok by som vam priblizila nejake pravidla derivovania. Derivacie su hlavne o vzorcekoch ktore si treba zapametat a potom ste z vecsej miery za vodou.

Zakladny vzorec derivovania je:

(xⁿ)' = n . x ^n-1 

• Priklad 1: (3x⁴)' = 12x³
• Toto je derivacia prveho stupna kedy exponentom nasobime cislo pred x a exponent sa nam znizuje o 1. Treba si dat pozor pri zapornych cislach pretoze znizenie znamena vecsi zapor. CIze keby sme v nasom 1.priklade  zmeili exponent na  -4 dostali by sme vysledok: -12x^-5 . Ako v kazdej matematickej operacii, znamienka su stale zavadzajuce preto si na nich treba dat fakt velkeho bacha .
• Taktiez si treba zapametat ze derivaciou samotneho X pri cisle je 0 a derivaciuou cisla bez X je 0
• Priklady: derivaciou 6x je 6, derivaciou 6 je 0
• Priklad 2: (6x³ - 2x² +3x - 5)' = 18x² + 4x + 3

Vzorec pre derivacie sucinu dvoch funkcii: 

(f . g)' = f' . g + f . g'

• Vypocet 1. derivacie
• Priklad 3: 1/8 (4x3 + 6x2 +6x + 3) . e^-2x)' =
• konstantu ktora sa nachaza pred prikladom nederivujeme !
• = 1/8 (12x² + 12x +6) . (e^-2x) + (-2e^-2x). (4x³ + 6x² + 6x +3) = 
• vyraz vieme upravit tak, ze s -2 v tretej zatvorke vynasobime 4 zatvorku a vytkneme e^_-2x, cize vyraz bude po upravach vyzerat nasledovne
• = 1/8 (12x² + 12x +6 - 8x³ -12x² -12x -6) . e^-2x =
• teraz pokratime co sa da, a kedze uz nederivujeme berieme do uvahy aj konstantu
• = 1/8 (12x² + 12x +6 - 8x³ -12x² -12x - 6) . e^-2x = -x³ . e^-2x

• Vypocet 2. derivacie (pouzijeme rovnaky vzorec ako pri 1. derivacii)
• (-x³ . e ^-2x)'' = (-3x² . e-^2x) + (-x³) . (-2e^-2x) = (-3x² + 2x³) . e^-2x
• tento tvar by sme mohli pouzit ako vysledok ale kedze je to matika a hladame co najjednoduchsie riesenie tak vytkneme x² a dostaneme x². (-3 + 2x ) . e^-2x

• Vypocet 3. derivacie 
• pri tomto vypocte je pre nas jedoduchsie pocitat s tvarom, ktory je zapisany ako sucin 2 fukncii, cize (-3x² + 2x³) . e^-2x 
• opat pouzijeme rovnaky vzorec a derivujeme
• ((-3x² + 2x³) . e^-2x)''' = (-6x + 6x²) . (e^-2x) + (-3x² + 2x³) . e^-2x = (-6x + 6x² + 6x² - 4x³) . e^-2x = (-4x³ + 12x² - 6x) . e^-2x
• a takto si mozeme derivovat dalej kym sa to len bude dat . Je to sranda ze? A to sme ani poriadne nezacali

Vzorec pre vypocet podielu dvoch funkcii 

(f/g)' = (f' . g - f . g' ) / (g²)

• Zakladnym pravidlom pri tomto vzorci je ze pocitame IBA S CITATELOM. Po upraveni vyrazu na tvar vzorca dame menovatel do tvaru g² uz to tak nechame az do konca prikladu. Zmeni sa iba ak budeme robit druhu derivaciu a znova pouzijeme vzorec. potom dostaneme g⁴
• Tentokrat tu priklad vlozim obrazok, bude to prehladnejsie, teda aspon dufam 

• 

• Ako si mozeme vsimnut nie je v tom ziaden chytak, treba si len davat pozor na znamienka 

Derivacie zlozenej funkcie 

g(x) = h(f(x))

(h(f(x))' = h' (f(x)) . f'(x)

• Tento vzorec sa moze javit trochu zlozito ale v skutocnosti tomu tak nie je . Vzjadruje nam sucin vonkajsej funkcie h a vnuternej funkcie f ysvetlime si to na priklade 5.
• Priklad 5: g(x) = sin (x² + 2x - 7)
• je dobre si niekam nabok napisat, ktora cast vyrazu je povazovana za funkciu vonkajsiu vonkajsiu a ktora za vnutornu. V nasom pripade oznacime h(x) = sinx a f(x) = x²+2x-7
• g'(x) = cos (x² + 2x -7) . (2x + 2) = 2(x+1) . cos (x² + 2x -7 )

• Priklad 6:  (e^5x)' = 5.e^5x
• h(x) = e^x , f(x) = 5x

•  Priklad 7: g(x) = ln (3 + 5cos3x) !!!
• tento priklad je zavadzajuci preto, lebo sa v nom vyskytuje trosku viac derivovania. Na prvy kohlad vidime, ze je to vzorec uvedeny hore, ale nestaci ho pouzit len raz. 
• Na zaciatok si oznacime h(x) = ln a f(x) = 3 + 5cos3x a povieme si ich derivacie. 
• Ze (ln)' = 1/x je nam vsetkym jasne, ale co s tym druhym vyrazom? Ako si mozeme vsimnut, vyraz 5cos3x je zlozena funkcia sama o sebe, preto ju treba vyriesit predym, nez sa pustime do riesenia celeho prikladu. (5 je povazovana za konstantu rpeto ju nederivujeme!)
• (3x)' = 3
• (cos3x)' = -sinx. 3x . 3 = -3sin3x 
• opat si urcujeme: h(x) = cos x , f(x) = 3x
• Z toho nam vyplyva ze pre povodny priklad bude platit ze f(x) = -3xin3x, takze pocitame:

• 

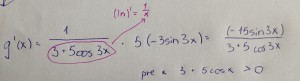
• Do derivacie prirodzeneho logarytmu sme za x dosadili nederivovanu funkciu f(x)

Tak a tymto mame za sebou tutorial na derivacie, tieto vzorce je potrebne vediet ako basnicku aj keby vas zobudili o polnoci  A este dolezitejsie je nielen ich vediet ale aj spravne pouzit   Ako dalsie sa pozrieme na vysetrovanie priebehu funkcii a parcialne derivacie