TIPY A HINTY
Snad najdolezitejsia cast, keru by mal kazdy dobry matik ovladat V tejto rubrike si povieme jak sa ma pocitat zdravo, ziadne hrotenie... sice nikoho pocitanie este nezabilo, ale naco riskovat
V tejto rubrike si povieme jak sa ma pocitat zdravo, ziadne hrotenie... sice nikoho pocitanie este nezabilo, ale naco riskovat takze tu uvediem zopar trikov jak si ulahcit zivot v matike hlavne v algebre, pri rieseni rovnic a zlomkov
takze tu uvediem zopar trikov jak si ulahcit zivot v matike hlavne v algebre, pri rieseni rovnic a zlomkov
Vecsina prikladov su chytaky na kere treba logicky, preto vzdy hladajte moznost jak dany zlomok vykratit alebo zjednodusit. Su aj caste pripady, profesori velmi casto take,  ktore musite najrv rozsirit aby ste vobec dostali vysledok
ktore musite najrv rozsirit aby ste vobec dostali vysledok Take pripady sa vecsinou riesia pouzitim "specialnej jednicky" ako mozme vidiet na priklade1. V tomto pripade je princip jednoduchy, ide o rozsirenie zlomku nasobenim tak aby sa cely zlomok nasledne vysledok nezmenil... Preto sa rozsiruje o jednicku, pretoze x.1=x pre hociktore x.
Take pripady sa vecsinou riesia pouzitim "specialnej jednicky" ako mozme vidiet na priklade1. V tomto pripade je princip jednoduchy, ide o rozsirenie zlomku nasobenim tak aby sa cely zlomok nasledne vysledok nezmenil... Preto sa rozsiruje o jednicku, pretoze x.1=x pre hociktore x.
Dalsi profesormi velmi oblubene priklady su na rozsirovanie  pouzitim "magickej nulky". Tento priklad som uvidol aj v limitach, takze vam to sem znovu hodim. Princip je znovu jednoduchy. Princip spociva v scitani alebo odcitani cisla, ktore chceme pouzit pri uprave prikladu tak, aby sme priklad nezmenili a teda ani jeho vysledok. Takze dane cislo bud scitame alebo odcitame, no po pricitani ho musime i odcitat a naopak, po odcitani ho musime znovu pricitat aby sme priklad nezmenili
pouzitim "magickej nulky". Tento priklad som uvidol aj v limitach, takze vam to sem znovu hodim. Princip je znovu jednoduchy. Princip spociva v scitani alebo odcitani cisla, ktore chceme pouzit pri uprave prikladu tak, aby sme priklad nezmenili a teda ani jeho vysledok. Takze dane cislo bud scitame alebo odcitame, no po pricitani ho musime i odcitat a naopak, po odcitani ho musime znovu pricitat aby sme priklad nezmenili Magia je v tom, ze ho mozete pripocitat kolko kcete, a priklad abo vysledok sa nezmeni. Supa ne?!?
Magia je v tom, ze ho mozete pripocitat kolko kcete, a priklad abo vysledok sa nezmeni. Supa ne?!? A zivot je hned o nieco snadnejsi...
A zivot je hned o nieco snadnejsi...
Teraz sa ale uz vratme ku krateniu a zjednodusovaniu. Najcastejsie pojde o kratenie podla vzorcekov:
-
a2 - b2 = (a - b)(a + b)
-
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
-
(a - b)2 = (a - b)(a - b) = a2 - 2ab + b2
-
(a + b)3 = a3 + 3a2b + 3ab2 + b3
-
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Dalsia uzitocna pomocka je vediet rozkladat zlomky, hodi sa hlavne pri intergraloch a derivaciach. Princip spociva v tom, ze priklad s velmi slozitym menovatelom nedokazeme vyriesit 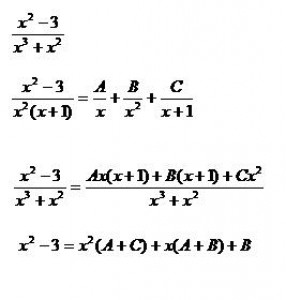 klasickym sposobom, alebo by bolo velmi narocne na cas. Preto sa menovatel rozlozi na niekolko mensich. Rozklada sa dovtedy kym nezahrnemie vsetky mocniny a cleny menovatela, takze neznamych nemusi byt iba 3 (A, B, C) ako mam v priklade ale moze ich byt aj 10, ale vecsinou sa v beznych prikladoch vyskytuju tak do 5 neznamych. Po uprave v poslednom kroku vidime ze
klasickym sposobom, alebo by bolo velmi narocne na cas. Preto sa menovatel rozlozi na niekolko mensich. Rozklada sa dovtedy kym nezahrnemie vsetky mocniny a cleny menovatela, takze neznamych nemusi byt iba 3 (A, B, C) ako mam v priklade ale moze ich byt aj 10, ale vecsinou sa v beznych prikladoch vyskytuju tak do 5 neznamych. Po uprave v poslednom kroku vidime ze
A + C = 1
A +B = 0
B = -3 ⇒ A =3 ⇒ C = -2 ⇒ takze vysledok rozkladu bude
Snad vam tieto triky a hinty pomozu vo vasom pocitani ci uz v skole abo v starobe, kazdopadne na vsetko treba logicky a troxu tricky aby ste neskoncili jak tento:
Komentáře
Přehled komentářů
20 mg sildenafil 680 <a href="https://vigrixvix.com/ ">viagra for women uk</a> https://vigrixvix.com/
brand cialis 20mg afhsdbcWhokmouttdzvcq
(knopsloh, 30. 5. 2021 23:25)purchasing cialis in canada https://rcialisgl.com/ - cialis paypale cialis onset of action
gsaxzvofbldEtelpBtjDorgou
(dryncAni, 30. 5. 2021 11:12)singulair canadian pharmacy https://pharmacyken.com/ - circle rx pharmacy imitrex canadian pharmacy
tnoegfdEtelpBtjDorgob
(beemeAsd, 26. 5. 2021 14:39)cialis soft tabs https://cialisjla.com/ - cialis seling cialis generic alternative
cvs pharmacy 24 hours dgsolbvfdWhokmouttathar
(knopsVed, 26. 5. 2021 14:15)other uses for cialis https://krocialis.com/ - online pharmacy cialis cost of cialis in mexico
sildenafil vs tadalafil which is better olgstnoegfdEtelpBtjDorgod
(Gtnbbeeme, 20. 5. 2021 14:34)how long does viagra take https://jokviagra.com/ - viagra vs cialis how to make homemade viagra
melrose pharmacy dgsolbvfdWhokmouttrhiuq
(Lbsoknops, 17. 5. 2021 16:01)cialis..com https://ucialisdas.com/ - herbal cialis gdzie kupić cialis
cialis overnighted afhsdbcWhokmouttajtzl
(Rebfknops, 15. 5. 2021 10:01)gnereic cialis https://rcialisgl.com/ canadian pharmacy no prescription cialis
medical pharmacy south fdvaefbfbldEtelpBtjDorgop
(Lebndrync, 14. 5. 2021 23:49)Celebrex https://xlnpharmacy.com/ canada drugs
viagra rezeptfrei in deutschland kaufen fhwsbbolthdEtelpBtjDorgok
(Fmrfdrync, 13. 5. 2021 21:24)cialis with out perscription https://cialisee.com/ - canadian cialis cialis online overnight
modafinil online pharmacy dgsolbvfdWhokmouttacrlv
(Lbsoknops, 11. 5. 2021 13:28)cialis buy online canada https://ucialisdas.com/ - tadalafil ( cialis ) cheap cialis tablets
Cefixime frbdcacldEtelpBtjDorgom
(Jebgdrync, 9. 5. 2021 0:58)cheap online pharmacy https://pharmacylo.com/ Oxytrol
Viagra capsules fdvaefbfbldEtelpBtjDorgob
(Lebndrync, 6. 5. 2021 23:30)costco online pharmacy https://xlnpharmacy.com/ meds online without doctor prescription
vente viagra sans ordonnance belgique fhwsbbolthdEtelpBtjDorgoy
(Fmrfdrync, 6. 5. 2021 22:01)cialis malaysia https://cialisee.com/ cialis professional legitimate
college pharmacy dgsolbvfdWhokmouttlmfww
(Lbsoknops, 4. 5. 2021 15:58)buy cialis on line overnight https://ucialisdas.com/ - i want to buy cialis in australia buy cialis 10 tab
levitra savings card fdvefbfbldEtelpBtjDorgon
(Lrbsdrync, 3. 5. 2021 10:32)buy levitra 20 mg https://uslevitraanna.com/ levitra dosage and administration
levitra 20mg cost per pill fbdcacldEtelpBtjDorgoy
(Jbsddrync, 28. 4. 2021 13:58)Super P-Force https://onlinecanda21.com/ Imuran
doctoral thesis database fhsbbolthdEtelpBtjDorgov
(Fbsfdrync, 25. 4. 2021 9:32)Hydrea https://uspharmus.com/ sildenafil citrate
generic cialis price hvgeahdEtelpBtjDorgof
(Brfgnelt, 31. 3. 2021 7:39)https://ljcialishe.com/ - cialis side effects with alcohol https://cialisvja.com/ - cialis information https://viagraonlinejc.com/ - viagra costs https://viagratx.com/ - viagra commercial girl https://buycialisxz.com/ - generic cialis canada
cialis what is it olgsanvoegfdEtelpBtjDorgox
(Grvbeeme, 30. 3. 2021 22:27)https://kloviagrli.com/ - when do you take viagra https://vigedon.com/ - lady viagra https://llecialisjaw.com/ - cialis reviews https://jwcialislrt.com/ - is there generic cialis https://jecialisbn.com/ - goodrx cialis
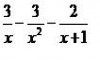


yhjrhitgndbegdrhanhofbldEtelpBtjDorgoy
(Wewerorma, 29. 7. 2022 9:04)