Goniometricke funkcie
Ako som uz spominal na konci rubriky o Pytagorovej vety, v tejto casti sa budem zaoberat goniometrickymi funkciami.
Definicia: Goniometricke funkcie vyjadruju vztah medzi velkostmi ostrych uhlov v pravouhlom trojuholniku a pomermi dlzok stran daneho trojuholniku... Mame trojuholnik ABC so stranami a,b,c:
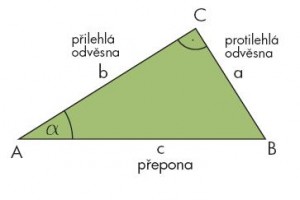
Plati potom vztahy :
:
Toto pravidlo by platilo i keby sme chceli pocitat uhol naprotilahlom uhlu, teda uhlu pri bode B. V tomto pripade by sa strana a zmenila na přilehlu odvěsnu a strana b by sa zmenila na protilehlú odvěsnu. NO sposob pocitania by zostal rovnaky.
Obcas je lepsie a prehladnejsie goniometricke funkcie vyjadrovat pomocou tzv. jednotkovej kruznice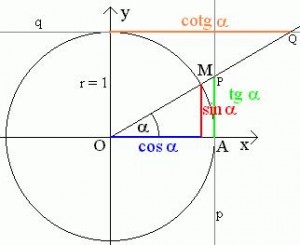 . Pomocou tejto kruznice su definovane funkcie sinus, cosinus, tangens a cotangens, kde mozme jasne vidiet vztahy odvesien a predpony.
. Pomocou tejto kruznice su definovane funkcie sinus, cosinus, tangens a cotangens, kde mozme jasne vidiet vztahy odvesien a predpony.
Pre jednoduchost pocitania je mozne casto najst tabulku pre zakladne vypocty goniometrickych funkcii, ktore prevadzaju goniometricke funkcie zakladnych uhlov ako je 0°, 30° ,45° ,60° ,90° do zlomkoveho tvaru pre jednoduchsie pocitanie. Kedze sa mi dost casto stava, ze potrebujem pocitat uhly zlozitejsie nez su zakladne preto sem uvediem rozsirenu tabulku .
Ako mozeme vidiet, su tu prevody na zlomky aj pre neobvykle uhly ako je 18° ,36° , 67° 37` , atd. Samozrejme takych to prepoctov goniometrickych funkcii do zlomkoveho tvaru je nespocetne vela a odvodit si ich mozete i s trochou goniometrickych znalosti i sami. No vecsinou vam budu staciet tie zakladne
Goniometricke funkcie sa daju ece pocitat pomocou nekonecnyc radov a limit. V tomto pripade konkretne podla Taylorovho radu.
fakta o goniometrickych fciach:
- funkcia sin(x) je vzdy neparna fcia, plati sin(-x) = - sin(x)
- funkcia cos(x) je vzdy parna fcia, plati cos(-x) = cos(x)
- funkcia tg(x) je vzdy neparna fcia, plati tg(-x) = - tg(x)
- funkcia cotg(x) je vzdy neparna fcia, plati cotg(-x) = - cotg(x)
a nakoniec... casto vyuzivane vzorce, ktore sa vam budu urco hodit:
Zakladne kere potrebujete pre zakladne operacie s goniometrickymi funkciami
A taktiez vzorce kere budete potrebovat menej, ale obcas sa celkom hodia
Komentáře
Přehled komentářů
stx21 encomo encomo encomo pensjonaty augustow noclegi pracownicze augustow noclegi augustow nad netta noclegi augustow u rycha noclegi w augustowie
DataFast Proxies | IPv6 Proxy for XEvil | Solver reCAPTCHA
(Floydhog, 17. 9. 2022 21:51)
<b>DataFast Proxies | IPv6 Proxy for XEvil | Solver reCAPTCHA</b>
<i><b>Definitive Solution in IPv6 Proxy! </b></i>
<i>Anonymous IPv6 Proxy, undetectable on L2 and L3 Layers of the OSI model,
100% no DNS leak, no Header leak.</i>
- Anonymous IPv6 proxy
- Undetectable IPv6 Proxy
- High Speed IPv6 Proxy
- Highest Quality IPv6 Proxy
- Virgin IPv6 proxy
- Dedicated IPv6 Proxy
- Rotating IPv6 Proxy
https://datafastproxies.com/
big pump signals
(Ernestfiege, 14. 9. 2022 1:27)
big pump signals
Of the main widgets, the last one remains: target 1-5, these are the goals of the coin pump, upon reaching which it is recommended to sell a digital token, for example, if you are a fan of quick profits, you can sell all pre-purchased coins at the values ​​​​of 1 goal in a trading signal. If you are willing to wait to earn more, place sell orders on the following targets and wait.
And here is the result of a successfully completed pump on the chart, in this example, three goals were achieved in less than 1 hour. VIP subscribers earned 18% profit on this, of course, you can achieve the same results.
Source:
- https://cryptopumpsignalsbinance.com/trading-news/profitable-trading-with-crypto-pump-signals-for-binance-telegram-group/
First flirt man site
(Barbarareday, 16. 7. 2022 13:02)Flirt In Love - https://2track.info/kJwk
Good girl domeprum
(domeprum 1080P, 13. 7. 2022 22:29)Hello, I'm good girl and looking for good man. If you are interested, I'll send my photo. Thank's https://tinyurl.com/2dm5ogc2
noclegi w augustowie z wyĹĽywieniem
(SobiEndonDak, 26. 6. 2022 2:24)
pokoje w Augustowie https://www.pokojew-augustowie.pl
podlaskie ciekawe noclegi https://www.pokojew-augustowie.pl/olx-noclegi-podlaskie
XEVIL 5.0: Nejlepší program pro řešení CAPTCHA je nyní k dispozici !
(RitaOl859, 19. 6. 2022 2:05)
XEvil 5.0 automaticky řeší většinu druhů captchas,
Včetně takového typu captcha: ReCaptcha-2, ReCaptcha v.3, Hotmail (Microsoft), Google captcha, Solve Media, BitcoinFaucet, Steam, +12k
+ hCaptcha podporováno v novém XEvil 6.0! Stačí vyhledat XEvil 6.0 na YouTube
Máte zájem? Jen google XEvil 5.0.15
P.S. Zdarma XEvil Demo je k dispozici !!
Taky, do 20. června je k dispozici Obrovská sleva: -30%!
XEvil.Net
Zkontrolujte nové video na YouTube:
"XEvil 6.0 <Beta>1] + XRumer multhithreading hCaptcha test"
נערות ליווי
(HenryOxymn23453, 18. 6. 2022 4:10)
"Right here is the perfect website for everyone who wishes to understand this topic. You realize a whole lot its almost hard to argue with you (not that I personally would want toOHaHa). You definitely put a brand new spin on a topic that has been written about for a long time. Wonderful stuff, just wonderful!"
https://israely-escort-ri.tk/news/olcopnepop
5 euro bonus ohne einzahlung
(belleriz , 10. 6. 2022 0:34)
https://www.leffatykki.com/profiili/soesoe/julkinen
https://www.woddal.com/post/827488_https-casinoacademy-net-de-die-top-5-liste-der-besten-online-casino-seiten-https.html
casino freispiele
online casinos mit 1 euro einzahlung
faires online casino
apartamenty komfort augustow
(PiCeataadado, 6. 6. 2022 7:41)https://www.noclegiiaugustow.online
mod menu grand theft auto v online
(belleriz, 1. 6. 2022 21:06)
https://www.youtube.com/watch?v=oryf0VlM15U&feature=youtu.be
https://youtu.be/feeXFD9duzY
gta v
gta 5 mod manager
gta 5 mod menu 2022,gta mod menu,gta 5 online mod menu,gta online mod menu,gta 5 mod menu pc,mod menu gta 5,gta 5 mod menu pc 2022,gta mod menu pc,gta online mod menu pc,gta 5 mod menu free,mod menu gta v online,gta 5 pc mod menu,gta online undetected menu,gta online mod menu free,gta 5 mod menu download pc,gta 5 mod menu download,gta mod menu free,kiddions mod menu,kiddions mod menu gta 5,gta 5 kiddions mod menu2022,gta v mod menu,gta 5 free mod menu,kiddions
june july free gta 5 hack, gta v hack 2022
gta 5 full game mobile download for ios android and windows 7, is gta 5 available for android phone, gta v mobile download gta 5 for android (apk-data-obb), gta 5 unity android ios download, gta 5 full game mobile download for ios android and windows, how to download unity on android, gta 5 official gameplay - prologue + download for android/ios, how to install gta v in mobile android, gta v mobile - download gta 5 for android & ios androidgtav.com, gta 5 unity android ios download free full version, gta v mobile - download gta 5 for android, gta 5 apk download for android and ios ppsspp highly compressed, gta 5 unity android ios download free, download gta 5 android ios free apk ipa, gta 5 download for android free full version ios 14, gta 5 unity android ios download free download, how to download and play gta 5 on android, how to download gta 5 on ios without verification, gta 5 download for android free full version ios, can you download gta 5 on ios, gta 5 apk download for android and ios ppsspp, can i download gta 5 on ios, how to download gta v game for android, download gta 5 android ios free apk ipa file, gta v mobile - download gta 5 for android & ios, how to download gta 5 on ios, can we download gta 5 in ios, is gta 5 available for android for free, can you download gta 5 on iphone, download gta 5 android ios free apk ipad, how to get android apk on ios, gta 5 on android download full game (android and ios), gta v mobile download gta 5 for android (apk-data-obb) gameplay, gta 5 download for android free full version ios 15, how to get gta v for android, how to gta v download in android mobile, how to download android apk on ios, gta 5 full game mobile download for ios android and windows free
hacks en gta 5
gta v
(belleriz, 1. 6. 2022 11:31)
https://www.furaffinity.net/journal/10232239/
https://www.youtube.com/watch?v=oryf0VlM15U&feature=youtu.be
hack para gta v
gta 5 mod menu xbox 1 download free
gta 5 mod menu 2022,gta mod menu,gta 5 online mod menu,gta online mod menu,gta 5 mod menu pc,mod menu gta 5,gta 5 mod menu pc 2022,gta mod menu pc,gta online mod menu pc,gta 5 mod menu free,mod menu gta v online,gta 5 pc mod menu,gta online undetected menu,gta online mod menu free,gta 5 mod menu download pc,gta 5 mod menu download,gta mod menu free,kiddions mod menu,kiddions mod menu gta 5,gta 5 kiddions mod menu2022,gta v mod menu,gta 5 free mod menu,kiddions
june july free gta 5 hack, gta v hack 2022
gta 5 full game mobile download for ios android and windows 7, is gta 5 available for android phone, gta v mobile download gta 5 for android (apk-data-obb), gta 5 unity android ios download, gta 5 full game mobile download for ios android and windows, how to download unity on android, gta 5 official gameplay - prologue + download for android/ios, how to install gta v in mobile android, gta v mobile - download gta 5 for android & ios androidgtav.com, gta 5 unity android ios download free full version, gta v mobile - download gta 5 for android, gta 5 apk download for android and ios ppsspp highly compressed, gta 5 unity android ios download free, download gta 5 android ios free apk ipa, gta 5 download for android free full version ios 14, gta 5 unity android ios download free download, how to download and play gta 5 on android, how to download gta 5 on ios without verification, gta 5 download for android free full version ios, can you download gta 5 on ios, gta 5 apk download for android and ios ppsspp, can i download gta 5 on ios, how to download gta v game for android, download gta 5 android ios free apk ipa file, gta v mobile - download gta 5 for android & ios, how to download gta 5 on ios, can we download gta 5 in ios, is gta 5 available for android for free, can you download gta 5 on iphone, download gta 5 android ios free apk ipad, how to get android apk on ios, gta 5 on android download full game (android and ios), gta v mobile download gta 5 for android (apk-data-obb) gameplay, gta 5 download for android free full version ios 15, how to get gta v for android, how to gta v download in android mobile, how to download android apk on ios, gta 5 full game mobile download for ios android and windows free
el mejor mod menu para gta nueva version
SUBIR NIVELES RAPIDO
(belleriz, 31. 5. 2022 23:31)
https://www.furaffinity.net/journal/10232239/
https://gta5mod.tiiny.site/
mod menu grand theft auto v online
gta 5 mod manager
gta 5 mod menu 2022,gta mod menu,gta 5 online mod menu,gta online mod menu,gta 5 mod menu pc,mod menu gta 5,gta 5 mod menu pc 2022,gta mod menu pc,gta online mod menu pc,gta 5 mod menu free,mod menu gta v online,gta 5 pc mod menu,gta online undetected menu,gta online mod menu free,gta 5 mod menu download pc,gta 5 mod menu download,gta mod menu free,kiddions mod menu,kiddions mod menu gta 5,gta 5 kiddions mod menu2022,gta v mod menu,gta 5 free mod menu,kiddions
june july free gta 5 hack, gta v hack 2022
gta 5 full game mobile download for ios android and windows 7, is gta 5 available for android phone, gta v mobile download gta 5 for android (apk-data-obb), gta 5 unity android ios download, gta 5 full game mobile download for ios android and windows, how to download unity on android, gta 5 official gameplay - prologue + download for android/ios, how to install gta v in mobile android, gta v mobile - download gta 5 for android & ios androidgtav.com, gta 5 unity android ios download free full version, gta v mobile - download gta 5 for android, gta 5 apk download for android and ios ppsspp highly compressed, gta 5 unity android ios download free, download gta 5 android ios free apk ipa, gta 5 download for android free full version ios 14, gta 5 unity android ios download free download, how to download and play gta 5 on android, how to download gta 5 on ios without verification, gta 5 download for android free full version ios, can you download gta 5 on ios, gta 5 apk download for android and ios ppsspp, can i download gta 5 on ios, how to download gta v game for android, download gta 5 android ios free apk ipa file, gta v mobile - download gta 5 for android & ios, how to download gta 5 on ios, can we download gta 5 in ios, is gta 5 available for android for free, can you download gta 5 on iphone, download gta 5 android ios free apk ipad, how to get android apk on ios, gta 5 on android download full game (android and ios), gta v mobile download gta 5 for android (apk-data-obb) gameplay, gta 5 download for android free full version ios 15, how to get gta v for android, how to gta v download in android mobile, how to download android apk on ios, gta 5 full game mobile download for ios android and windows free
el mejor mod menu gratis
hack para gta v
(belleriz, 31. 5. 2022 21:15)
https://youtu.be/feeXFD9duzY
https://dotnetfiddle.net/h1sTP0
gta 5 hack android
best gta 5 mod menu pc
gta 5 mod menu 2022,gta mod menu,gta 5 online mod menu,gta online mod menu,gta 5 mod menu pc,mod menu gta 5,gta 5 mod menu pc 2022,gta mod menu pc,gta online mod menu pc,gta 5 mod menu free,mod menu gta v online,gta 5 pc mod menu,gta online undetected menu,gta online mod menu free,gta 5 mod menu download pc,gta 5 mod menu download,gta mod menu free,kiddions mod menu,kiddions mod menu gta 5,gta 5 kiddions mod menu2022,gta v mod menu,gta 5 free mod menu,kiddions
june july free gta 5 hack, gta v hack 2022
gta 5 full game mobile download for ios android and windows 7, is gta 5 available for android phone, gta v mobile download gta 5 for android (apk-data-obb), gta 5 unity android ios download, gta 5 full game mobile download for ios android and windows, how to download unity on android, gta 5 official gameplay - prologue + download for android/ios, how to install gta v in mobile android, gta v mobile - download gta 5 for android & ios androidgtav.com, gta 5 unity android ios download free full version, gta v mobile - download gta 5 for android, gta 5 apk download for android and ios ppsspp highly compressed, gta 5 unity android ios download free, download gta 5 android ios free apk ipa, gta 5 download for android free full version ios 14, gta 5 unity android ios download free download, how to download and play gta 5 on android, how to download gta 5 on ios without verification, gta 5 download for android free full version ios, can you download gta 5 on ios, gta 5 apk download for android and ios ppsspp, can i download gta 5 on ios, how to download gta v game for android, download gta 5 android ios free apk ipa file, gta v mobile - download gta 5 for android & ios, how to download gta 5 on ios, can we download gta 5 in ios, is gta 5 available for android for free, can you download gta 5 on iphone, download gta 5 android ios free apk ipad, how to get android apk on ios, gta 5 on android download full game (android and ios), gta v mobile download gta 5 for android (apk-data-obb) gameplay, gta 5 download for android free full version ios 15, how to get gta v for android, how to gta v download in android mobile, how to download android apk on ios, gta 5 full game mobile download for ios android and windows free
hacks gta v
krynica morska noclegi blisko morza domki
(BeaiEndonDak, 16. 5. 2022 12:41)
hel tanie noclegi domki https://www.wakacjejeziorohancza.online
https://www.wakacjejeziorohancza.online/noclegi-krynki-sokoy-podlaskie-noclegi-podlaskie
valhtvfixmiz
(tadalafil drug, 2. 5. 2022 3:48)https://cialisusdc.com/ tadalafil side effects
ofmllohhvsrq
(cialis tadalafil, 29. 4. 2022 13:25)cialis cost https://extratadalafill.com/
Best website promotion services
(Seolfus, 29. 4. 2022 6:34)
I share with you professional website promotion services. The best price, the work is done within a few days. More than 1500 backlinks are created. Money back guarantee. A professional works through the kwork exchange https://kwork.com.
Here is the link https://kwork.com/offpageseo/13467403/professional-website-promotion-1500-good-back-links
qjxyemrurrex
(buy cialis online, 28. 4. 2022 11:15)cialis tadalafil https://nextadalafil.com/
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57
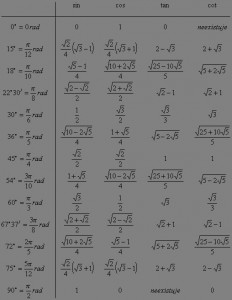
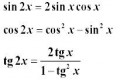

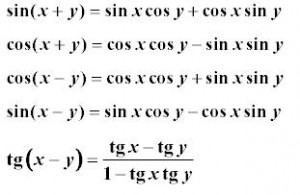
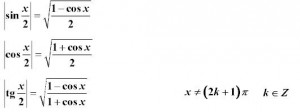


EndonDak encomo encomo
(WajtekEndonDak, 19. 9. 2022 11:59)