Pytagorova veta
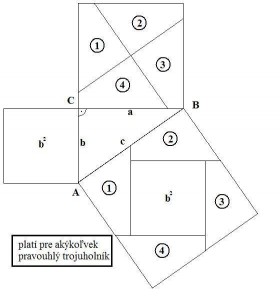
Pre pytagrovu vetu plati, ze obsah štvorca zostrojeného nad preponou (najdlhšou stranou) pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
a2 + b2 = c2
V pripade, ze by ste si chceli overit ze je to skutocne plati, som rozdelil stvorce nad priponou do nikolko casti a poskladal u predpony aby to pekne sedelo.
Samozrejme, tento sposob neplati iba pre stvorce ale pre hociktory utvar... pre inspiraciu vam sem hodim este niekolko moznosti.
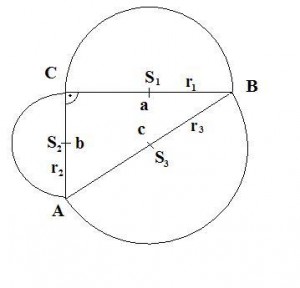
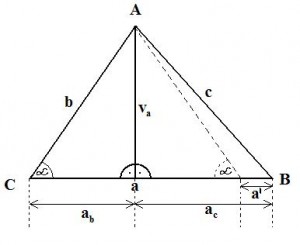
Napriklad v tomto pripade su sucty obsahov polkruhu nad priponou sa rovna obsahu polkruhu nad predponou. Alebo mozme povedat, ze vseobecne plati, ze sucet obsahov utvarov zostrojeneho nad priponami sa rovna obsahu utvaru zostrojeneho nad predponou A pre lenivejsich ako ja, ak by ste vobec nechceli pocitat vzorce na druhu, tak tu mate jednoduchy bezmocninovy vzorec na vypocet: Nesmieme ale zabudnut i na nepravouhle trojuholniky, pretoze i na nich je mozne vyuzit pytagorovu vetu. Takato veta sa nazyva uplna pytagorova veta a plati: c2 = a2 + b2 - 2.a.b.cosα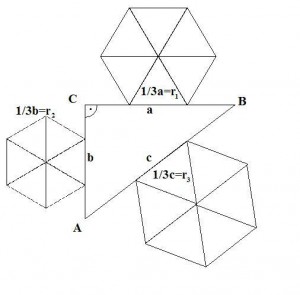

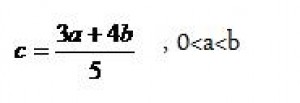
Teraz asi nastava otazka co je ten cosα goniometricke funkcie vysvetlim v nasledujucej rubrike
goniometricke funkcie vysvetlim v nasledujucej rubrike
Komentáře
Přehled komentářů
cialis dapoxetine 24 tab https://rcialisgl.com/ 10 mg cialis for sale
pharmacy times dgsolbvfdWhokmouttjovzw
(Lbsoknops, 13. 5. 2021 22:53)cialis/generic https://ucialisdas.com/ - all cialis drug original prices cialis 10mg vs 20mg
viagra pillen te koop fcsogsaxzvofbldEtelpBtjDorgot
(Anoodrync, 13. 5. 2021 19:23)ed pack viagra https://llviagra.com/ viagra tv commercial music
tadalafil drug interactions hvdgeeahdEtelpBtjDorgos
(Bbshnelt, 12. 5. 2021 15:15)buy viagra https://loxviagra.com/ viagra actress
where can i buy viagra on the high street fcsogsaxzvofbldEtelpBtjDorgoq
(Anoodrync, 12. 5. 2021 7:11)efectos malignos del viagra https://llviagra.com/ viagra tablets in malaysia
pharmacy boardshop dgsolbvfdWhokmouttpdtar
(Lbsoknops, 12. 5. 2021 5:35)i want to buy cialis in the uk https://ucialisdas.com/ indian cialis
ricetta del viagra fhwsbbolthdEtelpBtjDorgoz
(Fmrfdrync, 11. 5. 2021 22:51)cialis prescription online https://cialisee.com/ viagra/cialis
Exelon frbdcacldEtelpBtjDorgoc
(Jebgdrync, 8. 5. 2021 23:55)best drugstore bb cream https://pharmacylo.com/ web pharmacy
weac viagra fhwsbbolthdEtelpBtjDorgow
(Fmrfdrync, 8. 5. 2021 20:37)indian cialis https://cialisee.com/ female cialis
que es tadalafil olgstnoegfdEtelpBtjDorgom
(Gtnbbeeme, 7. 5. 2021 7:50)how to take viagra https://jokviagra.com/ viagra cialis
husband taking viagra fcsogsaxzvofbldEtelpBtjDorgow
(Anoodrync, 5. 5. 2021 3:17)viagra vs garlic https://llviagra.com/ - viagra a los 50 difference between viagra and shilajit
doença de peyronie e viagra fhwsbbolthdEtelpBtjDorgok
(Fmrfdrync, 4. 5. 2021 19:23)cialis dosage frequency https://cialisee.com/ - how much is cialis without insurance? black cialis sale
well care pharmacy dgsbvfdWhokmouttxsern
(Lhdvknops, 2. 5. 2021 15:53)buy cialis online https://asciled.com/ - cialis payment with paypal cialis 36 hour
online thesis writing fcsgsaxzvofbldEtelpBtjDorgov
(Abdgdrync, 2. 5. 2021 3:19)price pro pharmacy canada https://canadianeve21.com/ - Neurontin costco online pharmacy
cialis lilly icos tadalafil hvgeeahdEtelpBtjDorgom
(Bbdfnelt, 2. 5. 2021 2:32)viagra for sale ebay https://gensitecil.com/ - viagra gif how to use viagra for best results
tadalafil 40 mg with dapoxetine 60 mg olgsasbnvoegfdEtelpBtjDorgoe
(Gvdbbeeme, 27. 4. 2021 4:02)tadalafil soft https://boxtadafil.com/ tadalafil 5mg generic from us
cialis price costco olgsanvoegfdEtelpBtjDorgoh
(Grvbeeme, 30. 3. 2021 19:46)https://kloviagrli.com/ - does viagra work for women https://vigedon.com/ - viagra before and after photos https://llecialisjaw.com/ - is there a generic for cialis https://jwcialislrt.com/ - cialis from canada https://jecialisbn.com/ - cialis reddit
cialis coupon 2019 hvgeahdEtelpBtjDorgod
(Brfgnelt, 30. 3. 2021 13:54)https://ljcialishe.com/ - is there a generic for cialis https://cialisvja.com/ - cialis vs viagra cost https://viagraonlinejc.com/ - viagra vs sildenafil https://viagratx.com/ - alternative to viagra https://buycialisxz.com/ - cialis price walmart
Som buzerant a trtkám Každého oproti
(Som buzerant a trtkám do riti každého oproti , 19. 12. 2016 11:18)Kto chce sex ? Som panic a trtkám len chlapcov ktorý vedia pytagorovú vetu

viagra c20 cialis afhsdbcWhokmouttejicc
(Rebfknops, 15. 5. 2021 0:46)